Moin,
ich bin am Überlegen einen eigenen Darfblaster zu bauen. Die Feder soll dabei von einem Motor gespannt werden (ähnlich Stampede). Es geht dabei um Spaß am Basteln. Einfach das Innenleben eines anderen Blasters zu übernehmen kommt also nicht in Frage.
Nun zu meiner Frage. Wenn ich eine Feder mit einem Motor spannen will, wie viel Kraft müsste der Motor aufbringen?
Je höher die Übersetzung eines vorgeschalteten Getriebes, desto weniger Umdrehung hat der Motor natürlich, aber desto mehr Kraft steht zur Verfügung. Am Ende sollten etwa 90 bis 120 Umdrehungen die Minute rauskommen. Wenn wir davon ausgehen, dass eine Umdrehung die Feder komplett spannt.
Folgenden Aufbau nehme ich für die folgende Betrachtung an:
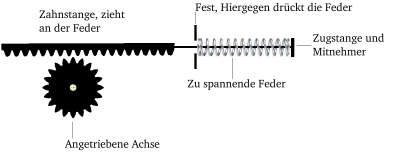
Dem Aufbau fehlt natürlich noch ein Mechanismus, damit die Feder schlagartig nach vorne schnellen kann. Dafür habe ich bereits Ideen, die die Skizze aber unnötig kompliziert machen würden.
Die Feder unter https://www.federnshop.com/de/produkte/druckfedern/vd-207j-73.html habe ich aktuell in meiner Stampede, also nutzen wir diese einfach für die folgende Fragestellung.
Die Feder hat eine Höchstkraft von knapp 60 Newton. Die Feder kann maximal 88 mm zusammengedrückt werden. Für die aktuelle Berechnung nehmen wir einmal 60 mm an.
Als Motor nehme ich einmal den folgenden https://www.conrad.de/de/universal-brushed-elektromotor-motraxx-x-drive-550-1-10500-umin-244465.html
Der Motor entspricht von der Größe her etwa dem, was in der Stampede verbaut ist.
Der Motor hat ca. 9000 RPM bei 7.2 V unter Belastung und maximal 4 Ncm Drehmoment. Wenn wir nun ein Getriebe mit einer Übersetzung von 1:100 verwenden bleiben am Ende noch etwa 90 RPM und wir haben 400 Ncm (Verluste durch das Getriebe ignoriert).
Nun haben wir zwei Werte und zwei verschiedene Einheiten. Die Feder hat 60 Newton und der Motor liefert bis zu 400 Newton-Zentimeter.
Ich habe bisher keine vernünftige Formel gefunden die beiden Werte mit einander zu vergleichen. nur etwas schwammig habe ich mal gelesen (leider keine Ahnung mehr wo), dass man die Ncm in N umrechnen kann, indem man das Drehmoment mit dem Achsdurchmesser verrechnet. x = Ncm / Umfang.
Wenn wir die das angetriebene Zahnrad mal mit einem Umfang von 60 mm Auslegen, entspricht eine Umdrehung des Zahnrads einer gespannten Feder.
400 Ncm / 6 cm = 66 Newton.
Das reicht nun relativ knapp die Feder zu spannen. Es wurden ja keine Verluste durch das Getriebe berücksichtigt.
Wenn ich dass nun mit der Stampede vergleiche:
Getriebe der Stampede: https://blasted.de/threads/stampede-getriebeschaden-ihr-auch.5713/#post-102154
Ich habe eine Übersetzung von 1:102 errechnet.
Die Stampede die Feder mit einer halben Umdrehung auf und das letzte Zahnrad hat einen Umfang von ca. 132 mm.
Demnach müsste die Stampede ca. 60 Newton * 13,2 cm * 2 = 1584 Ncm liefern. Bzw. 15,5 Ncm bei ca. 9000 RPM = 1,5 Umdrehungen / Sekunde. Meine Stampede liefert ca. 1,5 Darts die Sekunde. Eventuell sogar mehr.
Das sind Werte die nicht hinkommen können!
Meine Frage ist nun, kann man die benötigte Kraft des Motors ermitteln? Meine bisherigen Erkenntnisse scheinen nicht korrekt zu sein.
ich bin am Überlegen einen eigenen Darfblaster zu bauen. Die Feder soll dabei von einem Motor gespannt werden (ähnlich Stampede). Es geht dabei um Spaß am Basteln. Einfach das Innenleben eines anderen Blasters zu übernehmen kommt also nicht in Frage.
Nun zu meiner Frage. Wenn ich eine Feder mit einem Motor spannen will, wie viel Kraft müsste der Motor aufbringen?
Je höher die Übersetzung eines vorgeschalteten Getriebes, desto weniger Umdrehung hat der Motor natürlich, aber desto mehr Kraft steht zur Verfügung. Am Ende sollten etwa 90 bis 120 Umdrehungen die Minute rauskommen. Wenn wir davon ausgehen, dass eine Umdrehung die Feder komplett spannt.
Folgenden Aufbau nehme ich für die folgende Betrachtung an:

Dem Aufbau fehlt natürlich noch ein Mechanismus, damit die Feder schlagartig nach vorne schnellen kann. Dafür habe ich bereits Ideen, die die Skizze aber unnötig kompliziert machen würden.
Die Feder unter https://www.federnshop.com/de/produkte/druckfedern/vd-207j-73.html habe ich aktuell in meiner Stampede, also nutzen wir diese einfach für die folgende Fragestellung.
Die Feder hat eine Höchstkraft von knapp 60 Newton. Die Feder kann maximal 88 mm zusammengedrückt werden. Für die aktuelle Berechnung nehmen wir einmal 60 mm an.
Als Motor nehme ich einmal den folgenden https://www.conrad.de/de/universal-brushed-elektromotor-motraxx-x-drive-550-1-10500-umin-244465.html
Der Motor entspricht von der Größe her etwa dem, was in der Stampede verbaut ist.
Der Motor hat ca. 9000 RPM bei 7.2 V unter Belastung und maximal 4 Ncm Drehmoment. Wenn wir nun ein Getriebe mit einer Übersetzung von 1:100 verwenden bleiben am Ende noch etwa 90 RPM und wir haben 400 Ncm (Verluste durch das Getriebe ignoriert).
Nun haben wir zwei Werte und zwei verschiedene Einheiten. Die Feder hat 60 Newton und der Motor liefert bis zu 400 Newton-Zentimeter.
Ich habe bisher keine vernünftige Formel gefunden die beiden Werte mit einander zu vergleichen. nur etwas schwammig habe ich mal gelesen (leider keine Ahnung mehr wo), dass man die Ncm in N umrechnen kann, indem man das Drehmoment mit dem Achsdurchmesser verrechnet. x = Ncm / Umfang.
Wenn wir die das angetriebene Zahnrad mal mit einem Umfang von 60 mm Auslegen, entspricht eine Umdrehung des Zahnrads einer gespannten Feder.
400 Ncm / 6 cm = 66 Newton.
Das reicht nun relativ knapp die Feder zu spannen. Es wurden ja keine Verluste durch das Getriebe berücksichtigt.
Wenn ich dass nun mit der Stampede vergleiche:
Getriebe der Stampede: https://blasted.de/threads/stampede-getriebeschaden-ihr-auch.5713/#post-102154
Ich habe eine Übersetzung von 1:102 errechnet.
Die Stampede die Feder mit einer halben Umdrehung auf und das letzte Zahnrad hat einen Umfang von ca. 132 mm.
Demnach müsste die Stampede ca. 60 Newton * 13,2 cm * 2 = 1584 Ncm liefern. Bzw. 15,5 Ncm bei ca. 9000 RPM = 1,5 Umdrehungen / Sekunde. Meine Stampede liefert ca. 1,5 Darts die Sekunde. Eventuell sogar mehr.
Das sind Werte die nicht hinkommen können!
Meine Frage ist nun, kann man die benötigte Kraft des Motors ermitteln? Meine bisherigen Erkenntnisse scheinen nicht korrekt zu sein.

